Representing and Manipulating Information

2.1.3 addressing and Byte Ordering

For program objects that span multiple bytes, we must establish two conventions: what the address of the object will be, and how we will order the bytes in memory.

• In virtually all machines, a multi-byte object is stored as a contiguous sequence of bytes, with the address of the object given by the smallest address of the bytes used.
• for ordering the bytes representing an object, there are two common conventions.

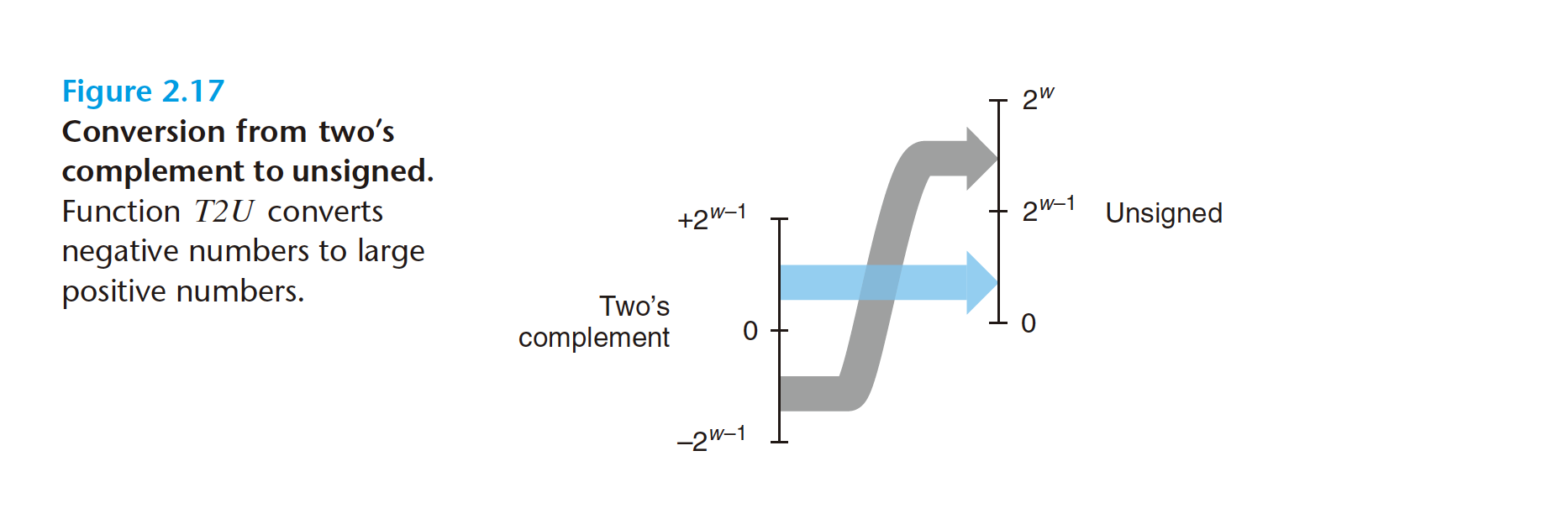
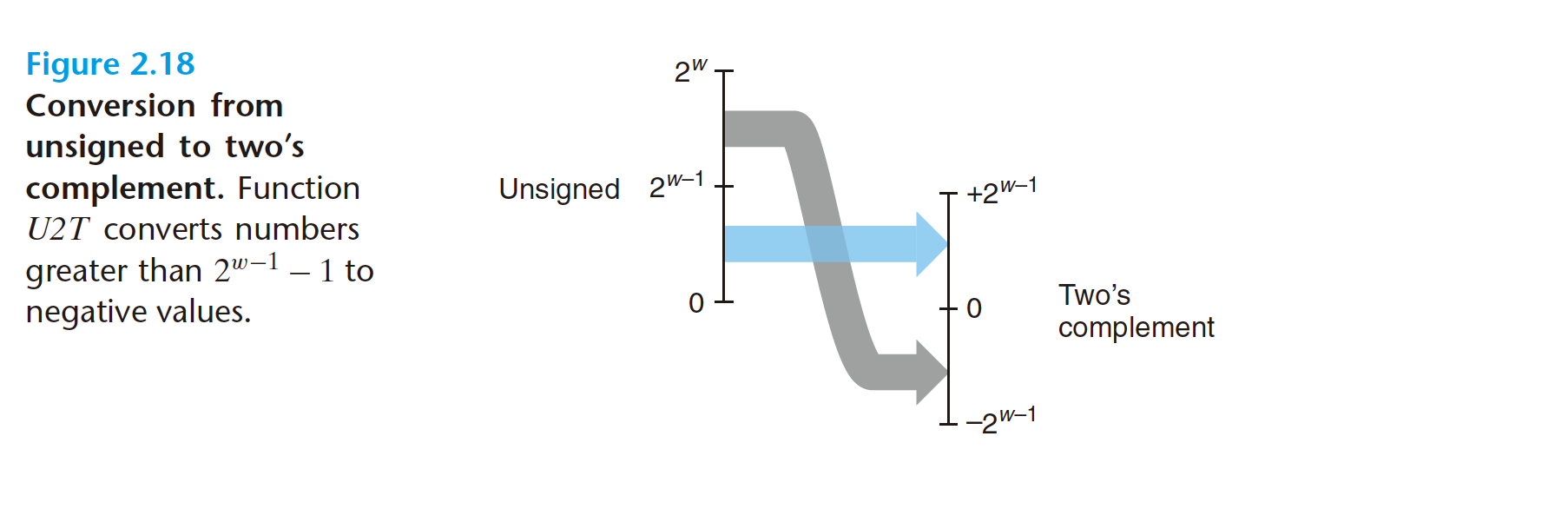
T2U

IEEE floating point

Case 1: Normalized Values
This is the most common case. It occurs when the bit pattern of exp is neither all zeros (numeric value 0) nor all ones (numeric value 255 for single precision, 2047 for double). In this case, the exponent field is interpreted as representing a signed integer in biased form. That is, the exponent value is E = e − Bias, where e is the unsigned number having bit representation e_k−1 . . . e₁e₀ and Bias is a bias value equal to 2^k−1 − 1 (127 for single precision and 1023 for double). This yields exponent ranges from −126 to +127 for single precision and −1022 to +1023 for double precision.
The fraction field frac is interpreted as representing the fractional value f , where 0 ≤f <1, having binary representation 0.f_n−1 . . . f₁f₀, that is, with the binary point to the left of the most significant bit. The significand is defined to be M = 1+ f . This is sometimes called an implied leading 1 representation, because we can viewM to be the number with binary representation 1.f_n−1f_n−2 . . . f₀. This representation is a trick for getting an additional bit of precision for free, since we can always adjust the exponent E so that significand M is in the range 1≤M <2 (assuming there is no overflow).We therefore do not need to explicitly represent the leading bit, since it always equals 1.

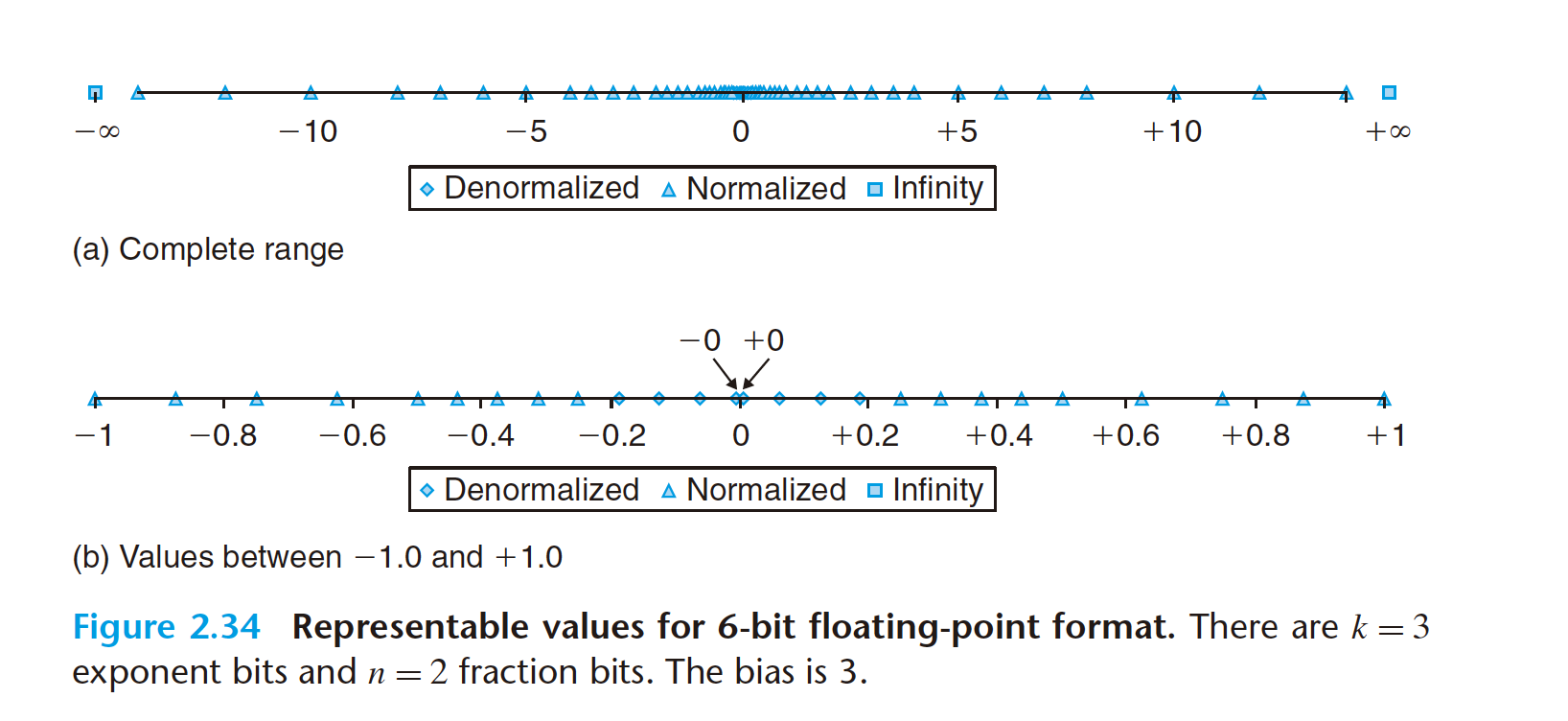
Case 2: Denormalized Values When the exponent field is all zeros, the represented number is in denormalized form. In this case, the exponent value is E = 1− Bias, and the significand value is M = f , that is, the value of the fraction field without an implied leading 1.
Denormalized numbers serve two purposes. First, they provide a way to represent numeric value 0, since with a normalized number we must always have M ≥ 1, and hence we cannot represent 0. In fact, the floating-point representation of +0.0 has a bit pattern of all zeros: the sign bit is 0, the exponent field is all zeros (indicating a denormalized value), and the fraction field is all zeros, giving M = f = 0. Curiously, when the sign bit is 1, but the other fields are all zeros, we get the value −0.0. With IEEE floating-point format, the values −0.0 and +0.0 are considered different in some ways and the same in others.
A second function of denormalized numbers is to represent numbers that are very close to 0.0. They provide a property known as gradual underflow in which possible numeric values are spaced evenly near 0.0.

Case 3: Special Values

---

2.4.3 example numbers